- Autor admin carl@lifeloveeveryday.com.
- Public 2023-12-16 19:17.
- Zadnja izmjena 2025-01-23 15:29.

Primeri zlatnog preseka mogu se naći svuda u klasičnoj arhitekturi, umetničkim delima, prirodi, pa čak i muzici. Ovaj izraz proporcije, poznat i kao božanski omjer, nudi harmoničnu kompoziciju primjenom iracionalnog broja (1.618) u dizajnu, kako prirodnom tako i ljudskom rukom. Najvjerovatnije niste svjesni matematike koja stoji iza ljepote zlatnog omjera jer proizvodi predmete i muziku za koje ćete prirodno smatrati da se sviđaju bez potrebe za objašnjenjem.
Zlatni rez u arhitekturi
Zlatni omjer stvara gotovo savršenu ljepotu u prirodi i umjetnosti. Kada počnete tražiti primjere zlatnog omjera u svakodnevnom životu, možda ćete biti iznenađeni brojnim primjerima koji su korišteni za stvaranje mnogih monumentalnih zgrada i struktura. Kada se zlatni omjer koristi u arhitekturi, kaže se da je zgrada stvorena korištenjem "svete arhitekture". Primjenom izračuna zlatnog omjera na kvadrat, arhitekte i dizajneri su u mogućnosti da stvore zlatni pravougaonik, za koji se vjeruje da ima najugodnije proporcije ljudskom oku.
Primjer zlatnog pravokutnika: Partenon

Fidija, grčki vajar, koristio je zlatni odnos u svom radu, posebno kada je počeo da radi sa bendovima koje je izvajao neposredno iznad Partenonskih stubova. Takođe je važno napomenuti da je numerička vrijednost dodijeljena zlatnom omjeru, Phi, nazvana u njegovu čast.
Ako izmjerite dimenzije eksterijera Partenona, otkrit ćete da on ne samo da čini zlatni pravougaonik, već da između stubova ima i mnogo zlatnih pravougaonika. Ova sveta građevina je prekrasan primjer zlatnog omjera u arhitekturi.
Primjer zlatnog trokuta: Velika piramida u Gizi
Zlatni omjer, zlatni pravougaonik i zlatni trougao mogu se naći u savršenstvu jednog od sedam svjetskih čuda, Velike piramide u Gizi. Da biste pronašli zlatni omjer, morat ćete prepoloviti kvadratnu osnovu piramide i nacrtati okomitu liniju do centra piramide. Kada se ovo poveže sa uglom stranom piramide, lako možete videti kako formira zlatni trougao sa omjerom 1,618, zlatnim omjerom.
Drugi arhitektonski primjeri
Možete pronaći mnogo primjera od drevne do moderne sakralne arhitekture i zgrada Zlatnog omjera.
- Chartres Cathedral - Centar, Francuska
- Notre Dame - Pariz, Francuska
- Djevojački trijem - Akropolj, Atina
- Taj Mahal - Agra, Indija
- Zgrada Ujedinjenih nacija - New York City, New York
Zlatni rez u primjerima umjetnosti
Možete pronaći mnoge primjere majstora slikara koji su koristili zlatni omjer. Ova djela savršenstva nastala su korištenjem omjera zlatnih pravokutnika i zlatnih trokuta. Umjetnost stvorena na temelju Zlatnog pravougaonika pokazala se ugodnijom ljudskom oku. To je jedna od misterija koje okružuju ovaj savršeni pravougaonik i zlatni omjer.
Zlatni rez u umjetnosti

Umjetnički primjeri zlatnog omjera uključuju:
- Leonardo Di Vinci - Mona Lisa, Vitruvian Man
- Botticelli - Rođenje Venere
- Mikelanđelo - Sveta porodica, ' David'
- Raphael - Crucifixion
- Rembrandt - Autoportret
- Salvador Dali - Sakrament posljednje večere, postojanost sjećanja
Korišćenje zlatnog omjera u umjetničkoj kompoziciji
Unutar zlatnog pravougaonika nalaze se određena područja koja su vizuelno privlačnija od drugih područja. Ove tačke se otkrivaju crtanjem linije od donjeg ugla pravougaonika do suprotnog ugla i ponavljanjem sa drugim donjim uglom. Ove linije će se ukrštati u tačno centru zlatnog pravougaonika. Zatim izmjerite sredinu duž svake linije počevši od središnje točke. Ove četiri tačke nazivaju se očima pravougaonika (zlatni rez). Glavna fokusna tačka slike je tada nacrtana ili oslikana unutar ovih interesnih tačaka (omjera).
Zlatni rez u muzici

Muzika se sastoji od numeričke vrijednosti i kada se zlatni omjer koristi za stvaranje muzičkog djela, postaje živi primjer matematike. Fibonačijeva sekvenca je takođe rasprostranjena u muzici:
- Postoji osam nota u skali.
- Treća i peta nota su osnova akorda.
- Dužina, ili oktava, bilo koje note je 13 nota.
Sekvencionisanje se nastavlja kroz muzičko delo i postaje složenije kako dostiže zlatni rez.
Kompozitori koji su koristili zlatni rez
Neki od najpoznatijih klasičnih kompozitora koristili su zlatni omjer i Fibonačijev niz u svojim muzičkim djelima, uključujući Bacha, Beethovena, Chopena i Mocarta. Neki moderni kompozitori poput Caseyja Mongovena istraživali su zlatni omjer u svojoj muzici.
Primjeri zlatnog omjera u prirodi

Gdje se zlatni omjer nalazi u prirodi? Nalazi se u zlatnoj ili Fibonačijevoj spirali, koja se može stvoriti korištenjem zlatnog omjera. Ovo je fenomen koji se u velikoj meri nalazi u prirodnom svetu. Listovi biljke rastu tako da što više njih može spiralno uzdignuti stabljiku. Novi list se formira tek nakon onog koji je formiran.
- Spiralni kaktusi
- Spiralne galaksije
- Suncokreti
Cvijeće sa Fibonačijevim nizom
Neko cvijeće ima latice cvijeća koje slijede Fibonačijev niz:
- Tri latice:Iris, ljiljan, orhideje, trilijum
- Pet latica: Buttercups, geraniums, hibiskus, Morning glory, nasturtium
- Osam latica: Delphiniums
- 13 latica: Određene sorte tratinčica, ambrozije, nevena
Fibonačijeva spirala u šišarkama

U zavisnosti od vrste drveća, takođe možete videti Zlatni odnos na delu unutar niza Fibonačijevih brojeva u šišarkama. Možete pronaći niz od osam spirala na jednoj strani šišarke, sa 13 spirala na drugoj. Drugi uzorak šišarki ima pet spirala na jednoj strani i osam na drugoj strani.
Zlatni rez u ljudima
Ovaj odnos je takođe važan ne samo za to kako ljudi gledaju jedni na druge, već i za način na koji njihova tela rade, i za njihov DNK.
DNK otkriva zlatni omjer
Jedan od najnevjerovatnijih primjera zlatnog omjera nalazi se unutar strukture ljudske DNK. Ovo se može vidjeti u jednom presjeku DNK koji otkriva da dvostruka spirala DNK formira desetokutni oblik. Ovo je kombinacija dva pentagona, rotirana za 36 stepeni jedan od drugog, formira dvostruku spiralu DNK. Sama spirala sa dvostrukom spiralom formira pentagon. Čak i jedan molekul DNK otkriva osnovu zlatnog preseka ili božanske proporcije.
Matematika iza zlatnog omjera
Pronalaženje zlatnog omjera u stvarnom životu je jednostavno, jer se pojavljuje svuda oko vas. To je matematički truizam koji se koristi za definiranje onoga što je opšte poznato kao savršeni broj koji se nalazi u prirodi, a koji su ljudi umnožavali i oponašali vekovima. Jednostavna ljepota ovog broja prikriva njegovu složenost u izvršenju. Da biste razumjeli teoriju koja stoji iza zlatnog omjera, prvo morate istražiti Fibonaccijevo sekvenciranje omjera.
Fibonačijev niz i zlatni omjer
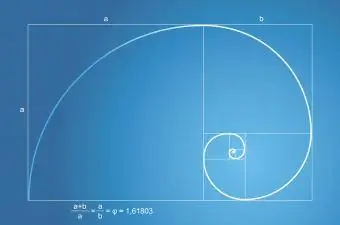
Fibonačijev niz ili niz ima odnos sa zlatnim rezom. Fibonačijev niz pokazuje se u broju listova na biljci i broju latica na cvijetu. Fibonačijeva spirala, koja se nalazi u prirodi, uvijek je dio zlatnog pravokutnika sa zlatnim omjerom.
Matematika Fibonačijevog niza je jednostavna:
- Sekvenca počinje sa 0 i 1.
- Samo zbrojite posljednja dva broja da dobijete sljedeći broj u nizu.
- 0+1=1, 1+1=2, 1+2=3, 2+3=5, 3+5=8, i tako dalje.
- Ovaj primjer Fibonačijevog niza postaje: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, i tako dalje.
Fibonačijev odnos prema zlatnom omjeru se ostvaruje kada se dodaje naprijed, dalje i dalje. Što više dodajete seriju, to ste bliže zlatnom omjeru.
Kreiranje zlatnog pravougaonika i trougla
Da biste kreirali zlatni pravougaonik sa Fibonačijevim nizom, počinjete sa kvadratom. Počet ćete graditi pravougaonik dodavanjem još jednog kvadrata originalnom kvadratu. Ne zaboravite da koristite formulu: 0+1=1 je prvi kvadrat, 1+1=2 - dodaćete još jedan kvadrat.1+2=3 ćete sabrati tri kvadrata, a sljedeće, 2+3=5, sabrat ćete pet kvadrata. Nastavit ćete sa dodavanjem kvadrata i na kraju formirati zlatni pravougaonik.
Zlatni trougao se može stvoriti prepolovljenjem Zlatnog pravougaonika od jednog ugla do suprotnog ugla. Ovo stvara trougao u kojem njegove tri strane ili uglovi imaju proporciju 2:2:1, što znači da su dvije dugačke stranice jednake po dužini, a kratki ugao je tačno polovina dužine dvije duže.
Zlatni rez u stvarnom svijetu
Zlatni omjer se često naziva božanskim omjerom zbog njegove istaknutosti u prirodi i ljudskim tijelima. Otkriće da je zlatni omjer prisutan u tolikom broju živih bića podstaklo je poštovanje prema ovoj magičnoj proporciji, te je i danas inspiracija za umjetnike i stvaraoce.






